Transformer:Transformer on Load

Transformer on Load

When the secondary is loaded, the secondary current I2 is set up. The V1 magnitude and phase of I2 with respect to V 2 is determined by the characteristics of the load. Current I2 is in phase with V2 if load is non-inductive, it lags if load is inductive and it leads if load is capacitive.

The secondary current sets up its own m.m.f. (=N2I2) and hence its own flux F2 which is in opposition to the main primary flux F which  due to I0. The secondary ampere-turns N 2 I2 are known as  demagnetising amp-turns. The opposing secondary flux F2 weakensth e primary flux F momentarily, hence primary back e.m.f. E1 tends to be I reduced. For a moment V 1 gains the upper hand over E1 and hence 2 causes more current to flow in primary. I0 Let the additional primary current be I2¢. It is known as load component of primary current. This current is antiphase with I2¢. The additional primary m.m.f. N1 I2 sets up its own flux F2¢ which is in I opposition to F2 (but is in the same direction as F) and is equal to it in magnitude. Hence, the two cancel each other out. So, we find that the magnetic effects of secondary current I2 are immediately neutralized by the additional primary current I2¢ which is brought into existence exactly at the same instant as I2. The whole process is illustrated in Fig. 32.17.

Hence, whatever the load conditions, the net flux passing through the core is approximately the same as at no-load. An important deduction is that due to the constancy of core flux at all loads, the core loss is also practically the same under all load conditions.

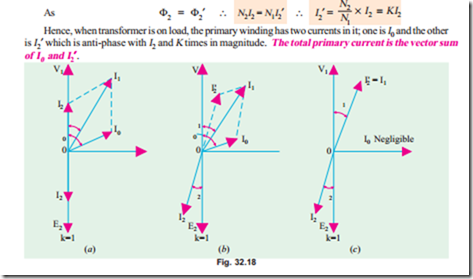
In Fig. 32.18 are shown the vector diagrams for a load transformer when load is non-inductive and when it is inductive (a similar diagram could be drawn for capacitive load). Voltage transformation ratio of unity is assumed so that primary vectors are equal to the secondary vectors. With reference to Fig. 32.18 (a), I2 is secondary current in phase with E2 (strictly speaking it should be V 2). It causes primary current I2¢ which is anti-phase with it and equal to it in magnitude (: K = 1). Total primary current I1 is the vector sum of I0 and I2¢ and lags behind V 1 by an angle f1.

In Fig. 32.18 (b) vectors are drawn for an inductive load. Here I2 lags E2 (actually V 2) by f2. Current I2¢ is again antiphase with I2 and equal to it in magnitude. As before, I1is the vector sum of I2¢ and I0 and lags behind V 1 by f1.

It will be observed that f1 is slightly greater than f2. But if we neglect I0 as compared to I2¢ as in Fig. 32.18 (c), then f1 = f2. Moreover, under this assumption

It shows that under full-load conditions, the ratio of primary and secondary currents is constant. This important relationship is made the basis of current transformer–a transformer which is used with a low-range ammeter for measuring currents in circuits where the direct connection of the ammeter is impracticable.

Example 32.12. A single-phase transformer with a ratio of 440/110-V takes a no-load current of 5A at 0.2 power factor lagging. If the secondary supplies a current of 120 A at a p.f. of 0.8 lagging, estimate the current taken by the primary.

 (Elect. Engg. Punjab Univ. 1991)

Example 32.14. A single phase transformer takes 10 A on no load at p.f. of 0.2 lagging. The turns ratio is 4 : 1 (step down). If the load on the secondary is 200 A at a p.f. of 0.85 lagging. Find the primary current and power factor.

Neglect the voltage-drop in the winding.

(Nagpur University November 1999)

Solution. Secondary load of 200 A, 0.85 lag is reflected as 50 A, 0.85 lag in terms of the primary equivalent current.

Tutorial Problems 32.2

1. The primary of a certain transformer takes 1 A at a power factor of 0.4 when it is connected across a 200-V, 50-Hz supply and the secondary is on open circuit. The number of turns on the primary is twice that on the secondary. A load taking 50 A at a lagging power factor of 0.8 is now connected across the secondary. What is now the value of primary current ?

[25.9 A]

2. The number of turns on the primary and secondary windings of a single-phase transformer are 350 and 38 respectively. If the primary winding is connected to a 2.2 kV, 50-Hz supply, determine

(a) the secondary voltage on no-load,

(b) the primary current when the secondary current is 200 A at 0.8 p.f. lagging, if the no-load current is 5 A at 0.2 p.f. lagging,

(c) the power factor of the primary current.

[239 V; 25-65 A; 0.715 lag]

3. A 400/200-V, 1-phase transformer is supplying a load of 25 A at a p.f. of 0.866 lagging. On no-load the current and power factor are 2 A and 0.208 respectively. Calculate the current taken from the supply.

 [13.9 A lagging V1 by 36.1°]

4. A transformer takes 10 A on no-load at a power factor of 0.1. The turn ratio is 4 : 1 (step down). If

a load is supplied by the secondary at 200 A and p.f. of 0.8, find the primary current and power factor (internal voltage drops in transformer are to be ignored).

 [57.2 A; 0.717 lagging]

5. A 1-phase transformer is supplied at 1,600 V on the h.v. side and has a turn ratio of 8 : 1. The transformer supplies a load of 20 kW at a power factor of 0.8 lag and takes a magnetising current of

2.0 A at a power factor of 0.2. Calculate the magnitude and phase of the current taken from the h.v. supply.

 [17.15 A ; 0.753 lag] (Elect. Engg. Calcutta Univ. 1980)

6. A 2,200/200-V, transformer takes 1 A at the H.T. side on no-load at a p.f. of 0.385 lagging. Calculate the iron losses.

If a load of 50 A at a power of 0.8 lagging is taken from the secondary of the transformer, calculate the actual primary current and its power factor.

[847 W; 5.44 A; 0.74 lag]

7. A 400/200-V, I-phase transformer is supplying a load of 50 A at a power factor of 0.866 lagging. The no-load current is 2 A at 0.208 p.f. lagging. Calculate the primary current and primary power factor.

[26.4 A; 0.838 lag] (Elect. Machines-I, Indore Univ. 1980)