Induction motor:Rotor Torque and Breakdown Torque

Rotor Torque and Breakdown Torque

The rotor torque at any slip s can be expressed in terms of the maximum (or breakdown) torque Tb by the following equation

Example 34.12. Calculate the torque exerted by an 8-pole, 50-Hz, 3-phase induction motor operating with a 4 per cent slip which develops a maximum torque of 150 kg-m at a speed of 660 r.p.m. The resistance per phase of the rotor is 0.5 W.

 (Elect. Machines, A.M.I.E. Sec. B, 1989)

Relation Between Torque and Slip

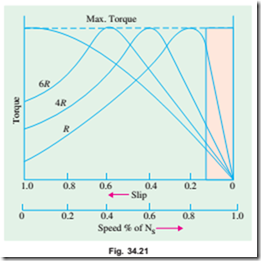
A family of torque/slip curves is shown in Fig. 34.21 for a range of s = 0 to s = 1 with R2 as the parameter. We have seen above in Art.

It is clear that when s = 0, T = 0, hence the curve starts from point O.

At normal speeds, close to synchronism, the term (s X2) is small and hence negligible w.r.t. R2. 4R

or T µ s if R2 is constant.

Hence, for low values of slip, the torque/slip curve is approximately a straight line. As slip increases (for increasing load on the motor), the torque when s = R2/X2. This torque is known as ‘pull-out’ or ‘breakdown’ torque Tb or stalling torque. As the slip further increases (i.e. motor speed falls) with further increase in motor load, then R2 becomes negligible as compared to (sX2.). Therefore, for large values of slip

Hence, the torque/slip curve is a rectangular hyperbola. So, we see that beyond the point of maximum torque, any further increase in motor load results in decrease of torque developed by the motor. The result is that the motor slows down and eventually stops. The circuit-breakers will be tripped open if the circuit has been so protected. In fact, the stable operation of the motor lies between the values of s = 0 and that corresponding to maximum torque. The operating range is shown shaded in Fig. 34.21.

It is seen that although maximum torque does not depend on R2, yet the exact location of Tmax is dependent on it. Greater the R2, greater is the value of slip at which the maximum torque occurs.