Computations and circle diagrams:Speed Control of Induction Motors

Speed Control of Induction Motors*

A 3-phase induction motor is practically a constant-speed machine, more or less like a d.c. shunt motor. The speed regulation of an induction motor (having low resistance) is usually less than 5% at full-load. However, there is one difference of practical importance between the two. Whereas d.c. shunt motors can be made to run at any speed within wide limits, with good efficiency and speed regulation, merely by manipulating a simple field rheostat, the same is not possible with induction motors. In their case, speed reduction is accompanied by a corresponding loss of efficiency and good speed regulation. That is why it is much easier to build a good adjustable-speed d.c. shunt motor than an adjustable speed induction motor.

Different methods by which speed control of induction motors is achieved, may be grouped under two main headings :

1. Control from stator side

(a) by changing the applied voltage

(b) by changing the applied frequency

(c) by changing the number of stator poles

2. Control from rotor side

(d) rotor rheostat control

(e) by operating two motors in concatenation or cascade

(f) by injecting an e.m.f. in the rotor circuit.

A brief description of these methods would be given below :

(a) Changing Applied Voltage

This method, though the cheapest and the easiest, is rarely used because

(i) a large change in voltage is required for a relatively small change in speed

(ii) this large change in voltage will result in a large change in the flux density thereby seriously disturbing the magnetic conditions of the motor.

(b) Changing the Applied Frequency

This method is also used very rarely. We have seen that the synchronous speed of an induction motor is given by Ns = 120 f/P. Clearly, the synchronous speed (and hence the running speed) of an induction motor can be changed by changing the supply frequency f. However, this method could only be used in cases where the induction motor happens to be the only load on the generators, in which case, the supply frequency could be controlled by controlling the speed of the prime movers of the generators. But, here again the range over which the motor speed may be varied is limited by the economical speeds of the prime movers. This method has been used to some extent on electrically- driven ships.

(c) Changing the Number of Stator Poles

This method is easily applicable to squirrel-cage motors because the squirrel-cage rotor adopts itself to any reasonable number of stator poles.

From the above equation it is also clear that the synchronous (and hence the running)speed of an induction motor could also be changed by changing the number of stator poles. This change of number of poles is achieved by having two or more entirely independent stator windings in the same slots. Each winding gives a different number of poles and hence different synchronous speed. For example, a 36-slot stator may have two 3-f windings, one with 4 poles and the other with 6-poles. With a supply frequency of 50-Hz, 4-pole winding will give Ns = 120 ´ 50/4 = 1500 r.p.m. and the 6- pole winding will give Ns = 120 ´ 50/6 = 1000 r.p.m. Motors with four independent stator winding are also in use and they give four different synchronous (and hence running) speeds. Of course, one winding is used at a time, the others being entirely disconnected.

This method has been used for elevator motors, traction motors and also for small motors driving machine tools.

Speeds in the ratio of 2:1 can be produced by a single winding if wound on the consequent-pole principle. In that case, each of the two stator windings can be connected by a simple switch to give two speeds, each, which means four speeds in all. For example, one stator winding may give 4 or 8-poles and the other 6 or 12-poles. For a supply frequency of 50-Hz, the four speeds will be 1500, 750, 1000 and 500 r.p.m. Another combination, commonly used, is to group 2- and 4-pole winding with a 6- and 12-pole winding, which gives four synchronous speeds of 3000, 1500, 1000 and 500 r.p.m.

(d) Rotor Rheostat Control

In this method (Fig. 35.36), which is applicable to slip-ring motors alone, the motor speed is reduced by introducing an external resistance in the rotor circuit. For this purpose, the rotor starter

may be used, provided it is continuously rated. This method is, in fact, similar to the armature rheostat control method of d.c. shunt motors.

(e) Cascade or Concatenation or Tandem Operation

In this method, two motors are used (Fig. 35.37) and are ordinarily mounted on the same shaft, so that both run at the same speed (or else they may be geared together).

The stator winding of the main motor A is connected to the mains in the usual way, while that of the auxiliary motor B is fed from the rotor circuit of motor A . For satisfactory operation, the main motor A should be phase-wound i.e. of slip-ring type with stator to rotor winding ratio of 1 : 1, so that, in addition to concatenation, each motor may be run from the supply mains separately.

here are at least three ways (and some- times four ways) in which the combination may be run.

1. Main motor A may be run separately from the supply. In that case, the synchronous speed is Nsa = 120 f / Pa where Pa = Number of stator poles of motor A .

2. Auxiliary motor B may be run separately from the mains (with motor A being disconnected). In that case, synchronous speed is Nsb = 120 ´ f / Pb where Pb = Number of stator poles of motor B.

3. The combination may be connected in cumulative cascade i.e. in such a way that the phase rotation of the stator fields of both motors is in the same direction. The synchronous speed of the cascaded set, in this case, is Nsc = 120 f/(Pa + Pb ).

How the Set Starts ?

When the cascaded set is started, the voltage at frequency f is applied to the stator winding of machine A . An induced e.m.f. of the same frequency is produced in rotor A which is supplied to auxiliary motor B. Both the motors develop a forward torque. As the shaft speed rises, the rotor frequency of motor A falls and so does the synchronous speed of motor B. The set settles down to a stable speed when the shaft speed becomes equal to the speed of rotating field of motor B.

Considering load conditions, we find that the electrical power taken in by stator A is partly used to meet its I2R and core losses and the rest is given to its rotor. The power given to rotor is further divided into two parts : one part, proportional to the speed of set i.e. N is converted into mechanical power and the other part proportional to (Nsa - N) is developed as electrical power at the slip frequency, and is passed on to the auxliary motor B, which uses it for producing mechanical power and losses.

Hence, approximately, the mechanical outputs of the two motors are in the ratio N : (Nsa - N). In fact, it comes to that the mechanical outputs are in the ratio of the number of poles of the motors.

It may be of interest to the reader to know that it can be proved that

As the differentially-cascaded set has a very small or zero starting torque, this method is rarely used. Moreover, the above expression for synchronous speed becomes meaningless for Pa = Pb.

Example 35.31. Two 50-Hz, 3-f induction motors having six and four poles respectively are cumulatively cascaded, the 6-pole motor being connected to the main supply. Determine the

frequencies of the rotor currents and the slips referred to each stator field if the set has a slip of 2 per cent. (Elect. Machinery-II Madras Univ. 1987)

Solution. Synchronous speed of set Nsc = 120 ´ 50/10 = 600 r.p.m. Actual rotor speed N = (1 - s) Nsc = (1 - 0.02) 600 = 588 r.p.m.

Synchronous speed of the stator field of 6-pole motor, Nsa = 120 ´ 50/6 = 1000 r.p.m. Slip referred to this stator field is

Example 35.33. The stator of a 6-pole motor is joined to a 50-Hz supply and the machine is mechanically coupled and joined in cascade with a 4-pole motor, Neglecting all losses, determine the speed and output of the 4-pole motor when the total load on the combination is 74.6 kW.

Solution. As all losses are neglected, the actual speed of the rotor is assumed to be equal to the synchronous speed of the set.

Now, Nsc = 120 ´ 50/10 = 600 r.p.m.

As said earlier, mechanical outputs are in the ratio of the number of poles of the motors.

output of 4-pole motor = 74.6 ´ 4/10 = 29.84 kW

Example 35.34. A cascaded set consists of two motors A and B with 4 poles and 6 poles respectively. The motor A is connected to a 50-Hz supply. Find

(i) the speed of the set

(ii) the electric power transferred to motor B when the input to motor A is 25 kW. Neglect losses.(Electric Machines-I, Utkal Univ. 1990)

Solution. Synchronous speed of the set is*

Nsc = 120 f/(Pa + Pb) = 120 ´ 50/(6 + 4) = 600 r.p.m.

(ii) The outputs of the two motors are proportional to the number of their poles.

output of 4-pole motor B = 25 ´ 4/10 = 10 kW

(f) Injecting an e.m.f. in the Rotor Circuit

In this method, the speed of an induction motor is controlled by injecting a voltage in the rotor circuit, it being of course, necessary for the injected voltage to have the same frequency as the slip frequency. There is, however, no restriction as to the phase of the injected e.m.f.

When we insert a voltage which is in phase opposition to the induced rotor e.m.f., it amounts to increasing the rotor resistance, whereas inserting a voltage which is in phase with the induced rotor e.m.f., is equivalent to decreasing its resistance. Hence, by changing the phase of the injected e.m.f. and hence the rotor resistance, the speed can be controlled.

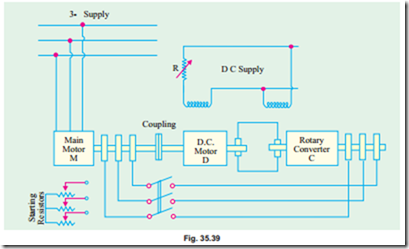
One such practical method of this type of speed control is Kramer system, as shown in Fig. 35.39, which is used in the case of large motors of 4000 kW or above. It consists of a rotary converter C which converts the low-slip frequency a.c. power into d.c. power, which is used to drive a d.c. shunt motor D, mechanically coupled to the main motor M.

The main motor is coupled to the shaft of the d.c. shunt motor D. The slip-rings of M are connected to those of the rotary converter C. The d.c. output of C is used to drive D. Both C and D are excited from the d.c. bus-bars or from an exciter. There is a field regulator which governs the back e.m.f. Eb of D and hence the d.c. potential at the commutator of C which further controls the slip- ring voltage and therefore, the speed of M.

One big advantage of this method is that any speed, within the working range, can be obtained instead of only two or three, as with other methods of speed control.

Yet another advantage is that if the rotary converter is over-excited, it will take a leading current which compensates for the lagging current drawn by main motor M and hence improves the power factor of the system.

In Fig. 35.40 is shown another method, known as Scherbius system, for controlling the speed of large induction motors. The slip energy is not converted into d.c. and then fed to a d.c. motor, rather it is fed directly to a special 3-phase (or 6-phase) a.c. commutator motor-called a, Scherbius machine.

The polyphase winding of machine C is supplied with the low-frequency output of machine M through a regulating transformer RT. The commutator motor C is a variable-speed motor and its speed (and hence that of M) is controlled by either varying the tappings on RT or by adjusting the position of brushes on C.

Tutorial Problems 35.5

1. An induction motor has a double-cage rotor with equivalent impedances at standstill of (1.0 + j 1.0) and (0.2 + j 4.0) W. Find the relative values of torque given by each cage (a) at starting and (b) at 5

% slip [(a) 40:1 (b) 0.4:1] (Adv. Elect. Machines AMIE Sec. B 1991)

2. The cages of a double-cage induction motor have standstill impedances of (3.5 + j 1.5) W and (0.6 + j 7.0) W respectively. The full-load slip is 6%. Find the starting torque at normal voltage in terms of full-load torque. Neglect stator impedance and magnetizing current.

[300%] (Elect. Machines-I, Nagpur Univ. 1993)

3. The rotor of a 4 pole, 50 Hz, slip ring induction motor has a resistance of 0.25 ohm per phase and runs at 1440 rpm at full-load. Calculate the external resistance per phase, which must be added to lower the speed to 1200 rpm, the torque being same as before.

[1 Wr] (Utilisation of Electric Power (E-8) AMIE Sec. B Summer 1992)