Alternators:Synchronous Reactance

By -
Synchronous Reactance

From the above discussion, it is clear that for the same field excitation, terminal voltage is decreased from its no-load value E0 to V (for a lagging power factor). This is because of

1. drop due to armature resistance, IRa

2. drop due to leakage reactance, IXL

3. drop due to armature reaction.

The drop in voltage due to armature reaction may be accounted for by assumiung the presence of a fictitious reactance Xa in the armature winding. The value of Xa is such that IXa represents the voltage drop due to armature reaction.

The leakage reactance XL (or XP) and the armature reactance Xa may be combined to give synchronous reactance XS.

Hence XS = XL + Xa*

Therefore, total voltage drop in an alternator

image

under load is = IRa + jIXS = I(Ra + jXS) = IZS where ZS is known as synchronous impedance of the armature, the word ‘synchronous’ being used merely as an indication that it refers to the working conditions.

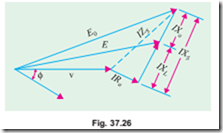
Hence, we learn that the vector difference between no-load voltage E0 and terminal voltage V is equal to IZS, as shown in Fig. 37.26.

Vector Diagrams of a Loaded Alternator

Before discussing the diagrams, following symbols should be clearly kept in mind.

E0 = No-load e.m.f. This being the voltage induced in armature in the absence of three factors discussed in Art. 37.16. Hence, it represents the maximum value of the induced e.m.f.

E = Load induced e.m.f. It is the induced e.m.f. after allowing for armature reaction. E is vectorially less than E0 by IXa. Sometimes, it is written as Ea (Ex. 37.16).

image

In Fig. 37.27 (a) is shown the case for unity p.f., in Fig. 37.27 (b) for lagging p.f. and in Fig. 37.27 (c) for leading p.f. All these diagrams apply to one phase of a 3-phase machine. Diagrams for the other phases can also be drawn similary.

Example 37.16. A 3-phase, star-connected alternator supplies a load of 10 MW at p.f. 0.85 lagging and at 11 kV (terminal voltage). Its resistance is 0.1 ohm per phase and synchronous reactance 0.66 ohm per phase. Calculate the line value of e.m.f. generated.

(Electrical Technology, Aligarh Muslim Univ. 1988)

image

Comments

Post a Comment

Popular posts from this blog

Total Loss in a D.C. Generator

By -
Image
Total Loss in a D.C. Generator The various losses occurring in a generator can be sub-divided as follows : where R a = resistance of armature and interpoles and series field winding etc. This loss is about 30 to 40% of full-load losses. Field copper loss. In the case of shunt generators, it is practically constant and I 2 R (or V I sh ). In the case of series generator, it is = I s e 2 R s e where R s e is resistance of the series field winding. This loss is about 20 to 30% of F.L. losses. (iii) The loss due to brush contact resistance. It is usually included in the armature copper loss. (b) Magnetic Losses (also known as iron or core losses), (i) hysteresis loss, W h µ B max f and ( ii ) eddy current loss, W e µ B max f These losses are practically constant for shunt and compound-wound generators, because in their case, field current is approximately constant. Both these losses total up to about 20 to 30% of F.L. losses. (c) Mechanica l Losses. These consist of :...
Read more

Transformer,three phase:Wye/Delta or Y/∆ Connection and Delta/Wye or ∆/Y Connection.

By -
Image
Wye/Delta or Y/∆  Connection The main use of this connection is at the substation end of the transmission line where the voltage is to be stepped down. The primary winding is Y -connected with grounded neutral as shown in Fig. 33.6. The ratio between the secondary and primary line voltage is 1/ 3 times the transformation ratio of each trans- former. There is a 30° shift between the primary and secondary line voltages which means that a Y - D transformer bank cannot be paralleled with either a Y - Y or a D - D bank. Also, third harmonic currents flows in the D to provide a sinusoidal flux. Delta/Wye or ∆/Y Connection This connection is generally employed where it is necessary to step up the voltage as for example, at the beginning of high tension transmission system. The connection is shown in Fig. 33.7. The neutral of the secondary is grounded for providing 3-phase 4-wire service. In recent years, this connection has gained considerable popularity because it can be used to s...
Read more

Testing of d.c.Machines:Brake Test

By -
Image
Brake Test It is a direct method and consists of applying a brake to a water-cooled pulley mounted on the motor shaft as shown in Fig. 31.1. The brake band is fixed with the help of wooden blocks gripping the pulley. One end of the band is fixed to earth via a spring balance S and the other is connected to a suspended weight W 1. The motor is running and the load on the motor is adjusted till it carries its full load current. The simple brake test described above can be used for small motors only, because in the case of large motors, it is difficult to dissipate the large amount of heat generated at the brake. Another simple method of measuring motor output is by the use of poney brake one form of which is shown in Fig. 31.2 ( a ). A rope is wound round the pulley and its two ends are attached to two spring balances S 1 and S 2. The tension of the rope can be adjusted with the help of swivels. Obviously, the force acting tangentially on the pulley is equal to the differ ence ...
Read more