Synchronous Motor:Constant-power Lines and Construction of V-curves.

Constant-power Lines

In Fig. 38.54, OA represents applied voltage / Yphase of the motor and AB is the back e.m.f. / phase, Eb. OB is their resultant voltage ER. The armature B current is OI lagging behind ER by an angle q = ER or vector OB represents (to some suitable scale) the main current I. OY is drawn at an angle f with OB (or at an angle q with C A). BL is drawn perpendicular to OX which is at right angles to O Y. Vector OB, when referred to O Y, also represents, on a different scale, the current both in magnitude and phase.

As V is constant, power input is dependent on B L. If motor is working with a constant intake, then locus of B is a straight line || to OX and ^ to OY i.e. line EF for which BL is constant. Hence, EF, represents a constant-power input line for a given voltage but varying excitation. Similarly, a series of such parallel lines can be drawn each representing a definite power intake of the motor. As regards these constant-power lines, it is to be noted that

1. for equal increase in intake, the power lines are parallel and equally-spaced

2. zero power line runs along OX

3. the perpendicular distance from B to OX (or zero power line) represents the motor intake

4. If excitation is fixed i.e. AB is constant in length, then as the load on motor is increased, increases. In other words, locus of B is a circle with radius = AB and centre at A. With increasing load, B goes on to lines of higher power till point B1 is reached. Any further increase in load on the motor will bring point B down to a lower line. It means that as load increases beyond the value corresponding to point B1, the motor intake decreases which is impossible. The area to the right of AY 1 represents unstable conditions. For a given voltage and excitation, the maximum power the motor can develop, is determined by the location of point B1 beyond which the motor pulls out of synchronism.

Construction of V-curves

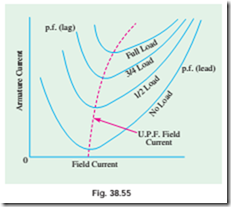
The V -curves of a synchornous motor show how armature current varies with its field current when motor input is kept constant. These are obtained by plotting a.c. armature current against d.c. field current while motor input is kept constant and are so called because of their shape (Fig. 38.55). There is a family of such curves, each corresponding to a definite power intake.

In order to draw these curves experimen- tally, the motor is run from constant voltage and constant-frequency bus-bars. Power input to motor is kept constant at a definite value. Next, field current is increased in small steps and corresponding armature currents are noted. When plotted, we get a V -curve for a particular constant motor input. Similar curves can be drawn by keeping motor input constant at different values. A family of such curves is shown in Fig. 38.55.

Detailed procedure for graphic construction of V -curves is given below :

1. First, constant-power lines are drawn as discussed in Art. 38.14.

2. Then, with A as the centre, concentric circles of different radii A B, A B1, A B2, etc. are drawn where A B, A B1, A B2, etc., are the back e.m.fs corresponding to different excitations. The intersections of these circles with lines of constant power give positions of the working points for specific loads and excitations (hence back e.m.fs). The vectors OB, OB1, OB2 etc., represent different values of ER (and hence currents) for different excitations. Back e.m.f. vectors A B, A B1 etc., have not been drawn purposely in order to avoid confusion (Fig. 38.56).

3. The different values of back e.m.fs like A B, A B1, A B2, etc., are projected on the magnetisation and corresponding values of the field (or exciting) amperes are read from it.

4. The field amperes are plotted against the corresponding armature currents, giving us ‘V ’ curves.