Speed control of d.c. Motors:Speed Control of Series Motors

By -

Speed Control of Series Motors

1. Flux Control Method

Variations in the flux of a series motor can be brought

about in any one of the following ways : Ia

(a) Field Divertors

The series winding are shunted by a variable resistance known as field divertor (Fig. 30.10). Any desired amount of current can be passed through the divertor by adjusting its resistance. Hence the flux can be decreased and consequently, the speed of the motor increased.

(b) Armature Divertor

A divertor across the armature can be used for giving speeds lower than the normal speed (Fig. 30.11). For a given constant load torque, if Ia is reduced due to armature divertor, the F must increase.

image

(c) Trapped Field Control Field

This method is often used in electric traction and is shown in Fig. 30.12.

The number of series filed turns in the circuit can be changed at will as shown. With full field, the motor runs at its minimum speed which can be raised in steps by cutting out some of the series turns.

(d) Paralleling Field coils

In this method, used for fan motors, several speeds can be obtained by regrouping the field coils as shown in Fig. 30.13. It is seen that for a 4-pole motor, three speeds can be obtained easily. (Ex.30.35)

image

2. Variable Resistance in Series with Motor

By increasing the resistance in series with the armature (Fig. 30.14) the voltage applied across the armature terminals can be decreased.

With reduced voltage across the armature, the speed is reduced. However, it will be noted that since full motor current passes through this resistance, there is a considerable loss of power in it.

image

Example 30.31. A d.c. series motor drives a load the torque of which varies as the square of the speed. The motor takes a current of 15 A when the speed is 600 r.p.m. Calculate the speed and the current when the motor field winding is shunted by a divertor of the same resistance as that of the field winding. Mention the assumptions made, if any. (Elect. Machines, AMIE Sec B, 1993)

image

image

Example 30.32. A 2-pole series motor runs at 707 r.p.m. when taking 100 A at 85 V and with the field coils in series. The resistance of each field coil is 0.03 W and that of the armature 0.04 W. If the field coils are connected in parallel and load torque remains constant, find (a) speed (b) the additional resistance to be inserted in series with the motor to restore the speed to 707 r.p.m.

image

image

Example 30.34. A 4-pole, series-wound fan motor runs normally at 600 r.p.m. on a 250 V d.c. supply taking 20 A. The field coils are connected at in series. Estimate the speed and current taken by the motor if the coils are reconnected in two parallel groups of two in series. The load torque increases as the square of the speed. Assume that the flux is directly proportional to the current and ignore losses. (Elect. Machines, AMIE, Sec B. 1990)

Solution. When coils are connected in two parallel groups, current through each becomes Ia2/2 where Ia2 is the new armature current.

image

Example 30.36. A d.c. series motor runs at 1000 r.p.m. when taking 20 A at 200 V. Armature resistance is 0.5 W. Series field resistance is 0.2 W. Find the speed for a total current of 20 A when a divertor of 0.2 W resistance is used across the series field. Flux for a field current of 10 A is 70 per cent of that for 20 A.

Solution. Eb1 = 200 - (0.5 + 0.2) ´ 20 = 186 V ; N1 = 1000 r.p.m.

Since divertor resistance equals series field resistance, the motor current of 20 A is divided equally between the two. Hence, a current of 10 A flows through series field and produces flux which is 70% of that corresponding to 20 A. In other words, F2 = 0.7 or F1/F2 = 1/0.7

image

Example 30.37. A 200 V, d.c. series motor takes 40 A when running at 700 r.p.m. Calculate the speed at which the motor will run and the current taken from the supply if the field is shunted by a resistance equal to the field resistance and the load torque is increased by 50%.

Armature resistance = 0.15 W, field resistance = 0.1 W

It may be assumed that flux per pole is proportional to the field.

image

Example 30.38. A 4-pole, 250 V d.c. series motor takes 20 A and runs at 900 r.p.m. Each field coil has resistance of 0.025 ohm and the resistance of the armature is 0.1 ohm. At what speed will the motor run developing the same torque if :

(i) a divertor of 0.2 ohm is connected in parallel with the series field

(ii) rearranging the field coils in two series and parallel groups Assume unsaturated magnetic operation.

(Electric Drives and their Control, Nagpur Univ. 1993)

Solution. The motor with its field coils all connected in series is shown in Fig. 30.15 (a). Here, N1 = 900 r.p.m., Eb1 = 250 - 20 ´ (0.1 + 4 ´ 0.025) = 246 V.

In Fig. 30.15 (b), a divertor of resistance 0.2 W has been connected in parallel with the series field coils. Let Ia2 be the current drawn by the motor under this condition. As per current-divider rule, part of the current passing through the series fields is Ia2 ´ 0.2/(0.1 + 0.2) = 2 Ia2/3. Obviously, F2 µ 2 Ia2/3.

image

(ii) In Fig. 30.15 (c), the series field coils have been arranged in two parallel groups. If the motor current is Ia2, then it is divided equally between the two parallel paths. Hence, F2 µ Ia2/2.

Since torque remains the same,

image

Example 30.39. A 4-pole, 230 V series motor runs at 1000 r.p.m., when the load current is 12 A. The series field resistance is 0.8 W and the armature resistance is 1.0 W. The series field coils are now regrouped from all in series to two in series with two parallel paths. The line current is now 20 A. If the corresponding weakening of field is 15%, calculate the speed of the motor.

(Electrotechnology-I, Guwahati Univ. 1987)

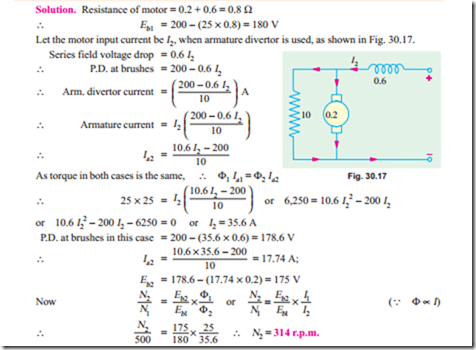
image

image

Example 30.40. A 200 V, d.c. series motor runs at 500 r.p.m. when taking a line current of 25 A. The resistance of the armature is 0.2 W and that of the series field 0.6 W. At what speed will it run when developing the same torque when armature divertor of 10 W is used ? Assume a straight line magnetisation curve. (D.C. Machines, Jadavpur Univ. 1988)

image

Example 30.41. A series motor is running on a 440 V circuit with a regulating resistance of R W for speed adjustment. The armature and field coils have a total resistance of 0.3 W. On a certain load with R = zero, the current is 20 A and speed is 1200 r.p.m. With another load and R = 3 W, the current is 15 A. Find the new speed and also the ratio of the two values of the power outputs of the motor. Assume the field strength at 15 A to be 80% of that at 20 A.

image

image

image

image

Comments

Post a Comment

Popular posts from this blog

Total Loss in a D.C. Generator

By -
Image
Total Loss in a D.C. Generator The various losses occurring in a generator can be sub-divided as follows : where R a = resistance of armature and interpoles and series field winding etc. This loss is about 30 to 40% of full-load losses. Field copper loss. In the case of shunt generators, it is practically constant and I 2 R (or V I sh ). In the case of series generator, it is = I s e 2 R s e where R s e is resistance of the series field winding. This loss is about 20 to 30% of F.L. losses. (iii) The loss due to brush contact resistance. It is usually included in the armature copper loss. (b) Magnetic Losses (also known as iron or core losses), (i) hysteresis loss, W h µ B max f and ( ii ) eddy current loss, W e µ B max f These losses are practically constant for shunt and compound-wound generators, because in their case, field current is approximately constant. Both these losses total up to about 20 to 30% of F.L. losses. (c) Mechanica l Losses. These consist of :...
Read more

Transformer,three phase:Wye/Delta or Y/∆ Connection and Delta/Wye or ∆/Y Connection.

By -
Image
Wye/Delta or Y/∆  Connection The main use of this connection is at the substation end of the transmission line where the voltage is to be stepped down. The primary winding is Y -connected with grounded neutral as shown in Fig. 33.6. The ratio between the secondary and primary line voltage is 1/ 3 times the transformation ratio of each trans- former. There is a 30° shift between the primary and secondary line voltages which means that a Y - D transformer bank cannot be paralleled with either a Y - Y or a D - D bank. Also, third harmonic currents flows in the D to provide a sinusoidal flux. Delta/Wye or ∆/Y Connection This connection is generally employed where it is necessary to step up the voltage as for example, at the beginning of high tension transmission system. The connection is shown in Fig. 33.7. The neutral of the secondary is grounded for providing 3-phase 4-wire service. In recent years, this connection has gained considerable popularity because it can be used to s...
Read more

Testing of d.c.Machines:Brake Test

By -
Image
Brake Test It is a direct method and consists of applying a brake to a water-cooled pulley mounted on the motor shaft as shown in Fig. 31.1. The brake band is fixed with the help of wooden blocks gripping the pulley. One end of the band is fixed to earth via a spring balance S and the other is connected to a suspended weight W 1. The motor is running and the load on the motor is adjusted till it carries its full load current. The simple brake test described above can be used for small motors only, because in the case of large motors, it is difficult to dissipate the large amount of heat generated at the brake. Another simple method of measuring motor output is by the use of poney brake one form of which is shown in Fig. 31.2 ( a ). A rope is wound round the pulley and its two ends are attached to two spring balances S 1 and S 2. The tension of the rope can be adjusted with the help of swivels. Obviously, the force acting tangentially on the pulley is equal to the differ ence ...
Read more