Elements of electromechanical energy conversion:Introduction,Salient aspects of conversions,Energy-balance,Magnetic-field system: Energy and Co-energy,Linear System,A Simple Electromechanical System,In terms of Field Energy.
Introduction
“Energy can neither be created nor be destroyed”. We can only change its forms, using appropriate energy-conversion processes.
An interesting aspect about the energy in “Electrical form” is that neither it is so available
![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjL1EZXt2-8e6PHbrZtEiEBAcZc60EE_9ecNZexIYLspt8-gEaPr1nbpAbU0Aki300PgyYzk1bKly61_mWMmtzf9Tb7URFUXctnI6dYBo4RPOWjZipdfCc73ktdm72pxWoUuUHFbQeBnCE/?imgmax=800)
Energy conversion takes place between well known pairs of forms of Energy: Electrical « Chemical, Electrical « Thermal, Electrical « Optical, Electrical « Sound, and Electrical « Mechanical are the common forms with numerous varieties of engineering - applications. Electrical « mechanical conversion is the focus of discussion in this chapter.
The elements of electro-mechanical energy conversion shall deal with basic principles and systems dealing with this aspect. Purpose of the study is to have a general approach to understand to design, and later to modify the system with the help of modern technologies, for overall improvisation.
It is necessary to be aware about:
(a) basic conditions to be fulfilled by the conversion system.
(b) methods for innovating the conversion systems.
Electromechanical energy-conversion finds applications in following categories of systems:
(a) transducers: Devices for obtaining signals for measurement / control,
(b) force-producing devices: Solenoid-actuators, relays, electromagnets,
(c) devices for continuous-energy-conversion: Motors / Generators
These systems have different configurations. But the principles of their working are common. Understanding these principles enables us to analyze / design / improvise / innovate such systems. As a result of such development, newer types of motors and the associated modern power controllers have recently been manufactured and become popular. Controllers using power electronics switching devices offer energy-efficient, user-friendly, and high-performance drives. Their initial investment may be larger but two important parameters justify their use: (i) Considerable energy is saved, resulting into payback periods as short as 18-24 months, (ii) The controllers ensure to limit the currents to pre-set values under conditions of starting /overload/ unbalanced supply. Hence, the entire system enjoys longer life. Both these effects lead to better production-process and hence these are readily acceptable by industries.
Salient Aspects of Conversions
Purpose of electro-mechanical conversion device is to change the form of energy. Here, for simpler discussion, only rotary systems will be dealt with. When it is converting mechanical input to electrical output the device is “generating”. With electrical input, when mechanical output is obtained, the device is motoring.
Some simple aspects of an electrical machine (motor / generator) have to be noted at this place:
(1) Electrical machine has a Stator, a Rotor, and an air-gap in between the two. For a flux path, the magnetic circuit has these three parts in series. In general, magnetic poles are established in Stator and in Rotor.
(2) Magnetic effects of following types can be categorized:
(a) Electromagnetic: Due to currents passed through windings on Stator and / or Rotor, producing certain number of poles on these members.
(b) Permanent Magnets: One side (Stator or Rotor) can have permanent magnets.
(c) Reluctance variation: Surface of Rotor near the air-gap can be suitably shaped to have a particular pattern of Reluctance- variation so as to control the machine behaviour as per requirements.
(3) Basic conditions which must be satisfied by such devices are:
(a) Equal number of poles must be created on the two sides.
(b) In some cases, reluctance-variation is primarily used for machine-action. The Stator side must accommodate a winding carrying current for the electromagnetic effect, when rotor surface is shaped so as to have the desired pattern of reluctance variation. Or, non-cylindrical rotor cannot have the current -carrying winding for machine action.
(4) Out of stator, rotor and air-gap, maximum energy-storage at any angular position takes place in the air-gap, since its reluctance is highest out of the three members.
(5) Stored energy must depend on rotor-position and the device tends to occupy that angular position which corresponds to maximum stored energy. If this position varies as a function of time, the device produces continuous torque.
(6) Ideal output of a motor is a constant unidirectional torque with given currents through its windings. In some cases, the output torque (as a compromise) is an average value of a cyclically varying torque.
(7) Where current-switching is done for motor-control, as in modern controllers, instantaneous effect has to be understood to conclude on any of the points mentioned above.
(8) A device can work either as a generator or as a motor, provided pertinent conditions are satisfied for the concerned mode of operation.
Energy – Balance
For an electro-mechanical system, following terms are important:
(i) Electrical port (= armature terminals): receiving / delivering electrical energy.
(ii) Mechanical port (= shaft): delivering / receiving mechanical energy.
(iii) Coupling field: Magnetic field or Electric field.
Even though, theoretically, both the types of fields mentioned above are able to convert the energy, the magnetic medium is most popular since the voltage levels required are not very high, and the devices of given power rating are smaller in size and are economical. Hence, only those will be dealt with.
It is obvious that an electrical motor receives energy at the electrical port and delivers it at the mechanical port. While an electric generator receives the energy at the mechanical port and delivers it at the electrical port. It is also known Conversion of electrical energy into mechanical energy that the following losses take place in such systems and are dissipated away as heat: (i) i2r losses in the windings of the machines, (ii) friction and windage losses, (iii) core-losses.
These can be either neglected or attached to electrical port, mechanical port and coupling magnetic field respectively, for simpler analysis. With this, the simple energy balance equation can be written as:
Change in Electrical Energy = Change in Mechanical Energy + Change in Field-Energy
It is natural that this equation has +ve signs for electrical and mechanical-energy-terms when the device is motoring. For generating mode, however, both the terms assume –ve signs.
In case no mechanical work is done, eqn. (25.1) reduces to eqn. (25.2) below indicating that Electrical energy - input is stored in the magnetic field.
Magnetic-field System: Energy and Co-energy
Linear System
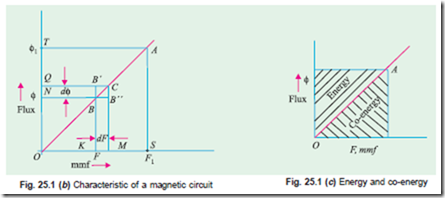
A simple magnetic current is shown in Fig 25.1 (a), with assumptions that air-gap length at the joints is negligible, and the magnetic medium is not saturated. With A as the cross-sectional area of the core and Lm as the mean length of the path, a coil with N turns carrying a current of i amp has an mmf of F, establishing a flux of f, related by
A Simple Electromechanical System
A simple electro-mechanical system is shown in Fig. 25.2(a).
Reference point O corresponds to the unstretched spring. Energy stored in the spring is then Zero. In position A of the movable member, the spring is elongated by x, and the corresponding energy stored in the spring is ½ Ks x2, where Ks is “spring-constant” of the linear system in Nw / m. In Fig 25.2 (a), the distance OA is x. The elemental distance AB is dx, so that OB is x + dx. For simpler analysis, it is assumed that magnetic material is highly permeable and that the clearance at point M (for movement of the member) is negligible. So that the mmf of the coil is required to drive the flux in the region OABC only. The flux-mmf
relationships are plotted for these two positions in Fig 25.2 (b). In position A, the movable member has moved a distance of x from its unstretched position or reference point. Let the operating point be H, so that the coil-mmf OA (=F) establishes a flux OB (=f). In this position, the movable member experiences a force in such a direction that the energy stored in the field tends to increase. It tends to reach B, so that an additional displacement of dx shifts the characteristic upwards and final operating point in position B is C . From H to C , the operating point can move in any one of the following ways:
(a) HC vertically, if the mechanical movement is too slow so that change of flux is slow and induced emf in the coil is negligible. This corresponds to the coil-mmf remaining constant at F during the transition. Constant mmf means vertical travel of the operating point from H to C .
(b) H to K horizontally and then K to C along the characteristic corresponding to (x + dx) as the displacement of the movable part. This is possible when the motion is very fast, resulting into flux remaining constant till the operating point traverses from H to K. Then, from K to C , the flux increases, an emf in induced the coil and the mmf finally reaches its value of F, at the point C´.
(c) In reality, the transition from H to C will be somewhere in between these two extremes mentioned above.
However, for simplicity, one of these extreme conditions has to be accepted. In (a) above, the mmf remains constant. In (b) above, the flux (and hence the flux-linkage) remains constant. Let us take the case of constant-mmf. If the process has taken a time of dt,
In terms of Field Energy








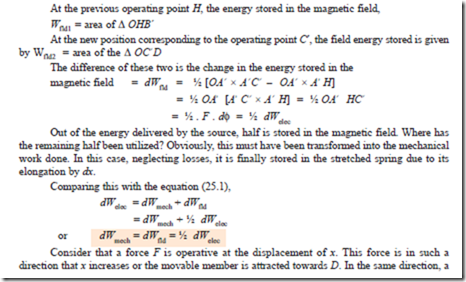




Comments
Post a Comment