Dynamic Equations and System-model of a Simple System

By -

Dynamic Equations and System-model of a Simple System

It is quite necessary to analyze electro-mechanical conversion system for predicting the performance and/or for monitoring the system. A simple system is being taken up here to deal with dynamic equations and a simple model with its components is being related to the system. The details will vary from system to system, and accordingly the equations will vary.

Fig. 25.7 shows different components of such a system meant for electrical to mechanical conversion. On one side, an electrical source feeds the device at the ‘electrical port’. On the other side, a force fe is developed at the ‘mechanical port’. Mechanical load is connected to this port.

(a) At Electrical Port : A voltage source is shown to feed the device. r is its effective internal resistance. At the electrical port, the inputs are l (= flux linkage with the coil) and i. From l , the voltage induced in the coil can always be evaluated.

(b) Role of the Conversion device: With these inputs, the device converts the energy into mechanical form, and is available as a force fe (in case of linear motions), and, displacement x measured from a suitable reference.

(c) At the Mechanical Port: The possible items are: spring, damper, mass and an applied mechanical force. Their natural and simple dependence on displacement x and its derivatives are indicated below:

image

The second term on the right-hand side is statically induced emf (or transformer-emf), since change of current with time is responsible for it. This cannot produce any force (or torque) and hence cannot convert energy from electrical to mechanical form (or vice-versa).

The third term on the right hand side includes the speed (= dx/dt) and dependence of L (x) on x. Any of these, if non-existent, will mean that third term reduces to zero. This term relates dynamically induced emf (= speed emf) and is the main indicator of the process of electro-mechanical energy conversion. So, for conversion, there must be an inductance which varies with the system position, and a motion must be there. In addition, coil must carry a current.

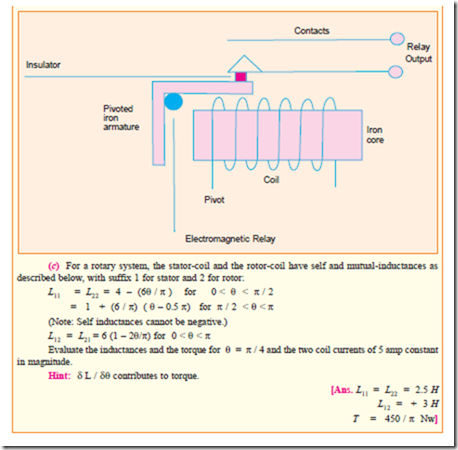
Having understood the linear-motion-system, it is easier to understand the system with rotary motion, with due modifications.

image

image

image

image

image

image

Comments

Post a Comment

Popular posts from this blog

Total Loss in a D.C. Generator

By -
Image
Total Loss in a D.C. Generator The various losses occurring in a generator can be sub-divided as follows : where R a = resistance of armature and interpoles and series field winding etc. This loss is about 30 to 40% of full-load losses. Field copper loss. In the case of shunt generators, it is practically constant and I 2 R (or V I sh ). In the case of series generator, it is = I s e 2 R s e where R s e is resistance of the series field winding. This loss is about 20 to 30% of F.L. losses. (iii) The loss due to brush contact resistance. It is usually included in the armature copper loss. (b) Magnetic Losses (also known as iron or core losses), (i) hysteresis loss, W h µ B max f and ( ii ) eddy current loss, W e µ B max f These losses are practically constant for shunt and compound-wound generators, because in their case, field current is approximately constant. Both these losses total up to about 20 to 30% of F.L. losses. (c) Mechanica l Losses. These consist of :...
Read more

Transformer,three phase:Wye/Delta or Y/∆ Connection and Delta/Wye or ∆/Y Connection.

By -
Image
Wye/Delta or Y/∆  Connection The main use of this connection is at the substation end of the transmission line where the voltage is to be stepped down. The primary winding is Y -connected with grounded neutral as shown in Fig. 33.6. The ratio between the secondary and primary line voltage is 1/ 3 times the transformation ratio of each trans- former. There is a 30° shift between the primary and secondary line voltages which means that a Y - D transformer bank cannot be paralleled with either a Y - Y or a D - D bank. Also, third harmonic currents flows in the D to provide a sinusoidal flux. Delta/Wye or ∆/Y Connection This connection is generally employed where it is necessary to step up the voltage as for example, at the beginning of high tension transmission system. The connection is shown in Fig. 33.7. The neutral of the secondary is grounded for providing 3-phase 4-wire service. In recent years, this connection has gained considerable popularity because it can be used to s...
Read more

Testing of d.c.Machines:Brake Test

By -
Image
Brake Test It is a direct method and consists of applying a brake to a water-cooled pulley mounted on the motor shaft as shown in Fig. 31.1. The brake band is fixed with the help of wooden blocks gripping the pulley. One end of the band is fixed to earth via a spring balance S and the other is connected to a suspended weight W 1. The motor is running and the load on the motor is adjusted till it carries its full load current. The simple brake test described above can be used for small motors only, because in the case of large motors, it is difficult to dissipate the large amount of heat generated at the brake. Another simple method of measuring motor output is by the use of poney brake one form of which is shown in Fig. 31.2 ( a ). A rope is wound round the pulley and its two ends are attached to two spring balances S 1 and S 2. The tension of the rope can be adjusted with the help of swivels. Obviously, the force acting tangentially on the pulley is equal to the differ ence ...
Read more