TESTING OF DC MACHINES

Testing of DC machines can be broadly classified as

i) Direct method of Testing
ii) Indirect method of testing

DIRECT METHOD OF TESTING:

In this method, the DC machine is loaded directly by means of a brake applied to a water cooled pulley coupled to the shaft of the machine. The input and output are measured and efficiency is determined by η=output/input . It is not practically possible to arrange loads for machines of large capacity.

INDIRECT METHOD OF TESTING:

In this method, the losses are determined without actual loading the machine. If the losses are known, then efficiency can be determined. Swinburne’s test and Hopkinson’s test are commonly used on shunt motors. But, as series motor cannot be started on No-load,these tests cannot be conducted on DC series motor.

(i) BRAKE TEST: is a direct method of testing.

In this method of testing motor shaft is coupled to a Water cooled pulley which is loaded by means of weight

as shown in figure4.1.

Wl= suspended weight in kg

W2 = Reading in spring balance in kg R = radius of pulley

N = speed in rps

V = Supply voltage

I = Full Load Current

Net pull due to friction = (Wl − W2) kg

= 9.81 (Wl − W2) Newton ………………. 1

Shaft torque T_sh = (W_l − W₂)R kg − mt.

This method of testing can be used for small motors only because for a large motor it is difficult to arrange for dissipation of heat generated at the brake.

(ii)Swinburne’s Test:

Figure 4.2

This test is a no load test and hence cannot be performed on series motor. The circuit connection is shown in Figure 4.2. The machine is run on no load at rated speed which is adjusted by the shunt field resistance.

ADVANTAGES

1. Economical, because no load input power is sufficient to perform the test
2. Efficiency can be pre-determined
3. As it is a no load test, it cannot be done on a dc series motor

DISADVANTAGES

1. Change in iron loss from no load to full load is not taken into account. (Because of armature reaction, flux is distorted which increases iron losses).

2. Stray load loss cannot be determined by this test and hence efficiency is over estimated.

3. Temperature rise of the machine cannot be determined.

4. The test does not indicate whether commutation would be satisfactory when the machine is loaded.

No load power input supplies

(i) Iron losses in the core

(ii) Friction and windings loss and

(iii) Armature copper loss.

Let I = load current at which efficiency is required

Ia = I – Ish if machine is motoring; I + Ish if machine is generating

Efficiency as a motor:

1. A 220 V DC shunt motor at No-load takes a current of 2.5 A. the resistance of the armature and shunt field are 0.8Ω and 200Ω respectively. Estimate the efficiency of the motor when the input current is 32 A.

2. A 440V D.C Shunt motor takes no load current of 25A. The resistance of shunt field and armature are550 Q & 1.2Q respectively. The full load line current is 32A. Determine the full load output &efficiency of the motor.

SOLUTION:input on no load= VI=440×2.5=1100W

2. A 500 V DC shunt motor when running on No-load takes 5 A. Armature resistance is 0.5Ω and shunt field resistance is 250Ω. Find the output in kW and η of the motor when running on full load and taking a current of 50 A.

(iii) Hopkinson’s Or Regenerative Or Back To Back Test:

This is a regenerative test in which two identical DC shunt machines are coupled mechanically and tested simultaneously. One of the machines is run as a generator while the other as motor supplied by the generator. The set therefore draws only losses in the machines. The circuit connection is shown in Figure 4.3. The machine is started as motor and its shunt field resistance is varied to run the motor at its rated speed. The voltage of the generator is made equal to supply voltage by varying the shunt field resistance of the generator which is indicated by the zero reading of the voltmeter connected across the switch. By adjusting the field currents of the machines, the machines can be made to operate at any desired load with in the rated capacity of the machines

ADVANTAGES:

i. The two machines are tested under loaded conditions so that stray load losses are accounted for.
ii. Power required for the test is small as compared to the full load powers of the two machines. Therefore economical for long duration tests like “Heat run tests”.
iii. Temperature rise and commutation qualities can be observed.
iv. By merely adjusting the field currents of the two machines the two machines can be loaded easily and the load test can be conducted over the complete load range in a short time.

DISADVANTAGES:

i. Availability of two identical machines
ii. Both machines are not loaded equally and this is crucial in smaller machines.
iii. There is no way of separating iron losses of the two machines which are different because of different excitations.
iv. Since field currents are varied widely to get full load, the set speed will be greater than rated values.

The efficiency can be determined as follows:

CIRCUIT DIAGRAM

ALTERNATIVE CONNECTION:

Figure 4.4

The Figure 4.4 shows an alternate circuit connection for this test. In this connection the shunt field windings are directly connected across the lines. Hence the input current is excluding the field currents. The efficiency is determined as follows:

1. The Hopkinson’s test on two similar shunt machines gave the following Full load data.Line voltage = 110 V; Line current = 48 A; Motor armature current = 230 A; Field currents are 3 A and

3.5 A; Armature resistanceof each machine is 0.035 Ω; brush drop of 1V/brush; Calculate the efficiency of each machine.

SOLUTION:

2. In a Hopkinson’s test on a pair of 500 V, 100 kW shunt generator. The following data was obtained:Auxiliary supply 30 A at 500 V; Generator output current 200 A; Field current 3.5 A and

1.8 A; ra = 0.075 Ω for each machine; voltage drop at brushes = 2 V/machine; calculate the efficiency of the machine as a generator.

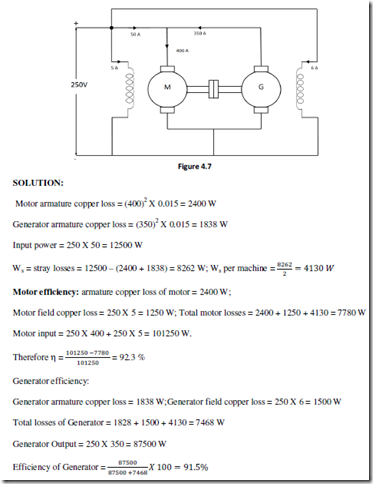
3. In a Hopkinson test on 250 V machine, the line current was 50 A and the motor current is 400 A not including the field currents of 6 and 5 A. the armature resistance of each machine was 0.015Ω. Calculate the efficiency of each machine.

4. The following test results were obtained while Hopkinson’s test was performed on two similar DC shunt machine. Supply voltage = 250 V; Motor Field Current = 2 A; Generator Field Current = 2.5A; Generator Armature Current = 60 A; Current taken by the two armature from supply = 15 A; Armature Resistance/Machine = 0.2Ω; Calculate the efficiency of motor and generator under these conditions.

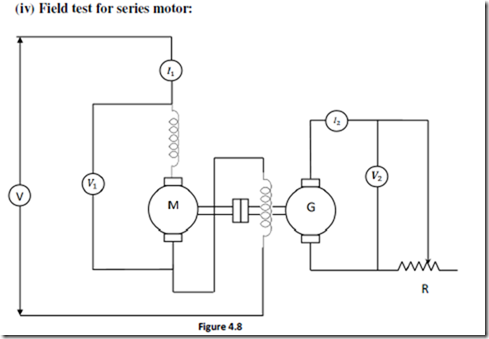
Figure 4.8 shows the circuit for fields test. This test is applicable to two similar series motor. One of the machine runs as a motor and drives a generator whose output is wasted in a variable load ‘R’. Both machine field coils are in series and both run at same speed so that iron and friction losses are made equal.

Load resistance ‘R’ is varied till the motor current reaches its full load value.

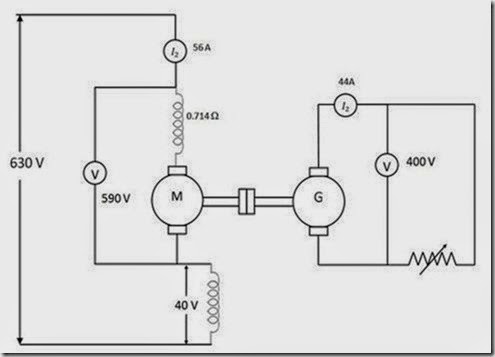
1. A test on two coupled similar tramway motors with their fields connected in series, gave the following results when one machine acted as a motor and the other as a generator.Motorarmature current = 56 A; Armature voltage = 550 V; Voltage drop across the field winding = 40V; Generator: armature current = 44 A; Armature voltage = 400 V; Field drop across the field winding = 40V; Resistance of each armature = 0.3Ω; Calculate the efficiency of motor and gearing at this load.

Figure 4.9

SOLUTION:

3. A field’s test on two similar series machines gave the following data; Motor: Armature current: 60A; Voltage across armature: 500V; Voltage across field: 40V; Generator: Terminal voltage: 450V; Output current 46A; Voltage across field:40V; Armature resistance of each machine is 0.25Q. Calculate the efficiency of both the machines.

SOLUTION:

Total input = 580×60=34800W Output =450×46=20700W

Therefore total losses in 2machines = 34800-20700=14100W

(V) Retardation or running down test:

This method is applicable to shunt motors and generators and is used for finding the stray losses. If armature and shunt copper losses are known for a given load, efficiency can be calculated. The circuit is shown in figure 4.11.

Machine is speeded up slightly beyond its rated speed and then supply is cut off from the armature while keeping the field excited. Armature will slow down and its kinetic energy is needed to meet rotational losses. i.e., friction and windage losses.

hence voltmeter reading falls. Voltage and time at different intervals are noted and a curve is drawn between the time and speed as shown in Figure 4.12.

(ii) Finding Moment of Inertial ‘I’: There are two methods of finding the moment of inertia ‘I’

(a) I is calculated:

(i) Slowing down curve with armature alone is calculated.

(ii) A fly wheel is keyed to the shaft and the curve is drawn again

(iii) For any given speed, dN, and dN are determined as before.

(b) I is eliminated: In this method, time taken to slow down is noted with armature alone and then a retarding torque is applied electrically i.e., a non inductive resistance is connected to the armature. The additional loss is /2(R + R)orV/ .

Let W1 be the power then

1. A retardation test is made on a separately excited. DC machine as a motor the induced voltage falls from 240V to 225V in 25 secs on opening the armature circuit & 6 secs on suddenly changing the armature connection from supply to a load resistance taking 10A (average). Find the efficiency of the machine when running as a motor& taking a current of 25A on a supply of 250V. The resistance of its arm is 0.4Ω & that of its field winding is 250Ω.

SOLUTION:

2. In a retardation test on a separately motor, the induced emf in the armature falls from 220V to 190V in 30seconds on disconnecting the armature from the supply. The same fall takes place in 20seconds if, immediately after disconnection, armature is connected to a resistance which takes 10A (average) during this fall, find the stray losses of motor.

SOLUTION:

(2) A retardation test is carried out on a 1000rpm D.C machine. The time taken for the speed to fall from 1030 rpm to 970rpm is (a) 36secs with no excitation. (b) 15secs with full excitation & (c) 9 seconds with full excitation & the armature supplying an extra load of 10A at 219V. Calculate (1) The moment of inertia of the armature is kg.m2. (2) Iron loss and (3) Themechanical losses at the mean speed of 1000rpm.

SOLUTION:

(i) When the arm slows down with no excitation its kinetic energy is used to over come mechanical losses only (no flux, no Iron loss)

(ii) With excitation, Kinetic Energy is used to supply mechanical & iron losses ie., stray losses.

(iii) If Moment of Inertia is in kgm2 unit then rate of loss of energy is in Watts.

4. In a retardation test on a DC motor with its field normally excited the speed fell from 1525 to 1475 rpm in 25seconds. With an average load of 1.0kw supplied by the armature, the same speed drop occurred in 20seconds. Find out the Moment of Inertia of the rotating parts in kg- m2.

SOLUTION:

Search This Blog

DC MACHINES course